这一期游戏专栏跟大家讲解一下抽卡游戏里卡牌掉落的概率模型。
现在随便点开手游的氪金营收榜里,最上面的往往都是以抽卡为主的游戏。这些游戏仿佛有着魔力一般吸引着人们的加入,并让如今的游戏商们赚的盆钵满盈。无疑,它是现今最有效果的赚钱招数。
首先,明确一个根本问题抽卡系统算法是不是做到了真随机——绝不是真随机,都是伪随机。
抽卡机制,其核心是数值策划的合理性。出极品的概率太低则玩家不愿意参与,出极品概率过高则玩家太容易满足,影响付费的持续性且缩短游戏体验周期。
—————————————————-分割线——————————————————–
如果使用纯随机的算法:
假设卡池中价值高概率低的物品,我们假设概率为5%,抽出的期望值为20次,然而实际情况下绝大部分玩家能在少数几次抽出,少部分玩家超过20次都没有出,这会导致玩家群体游戏差异较大。而且在模拟后的随机次数分布计算中,有5%的玩家一次就能抽出高价值物品,10次以内抽出的玩家可以达到40%,但是也有7%的玩家五十连抽也没有抽出来。
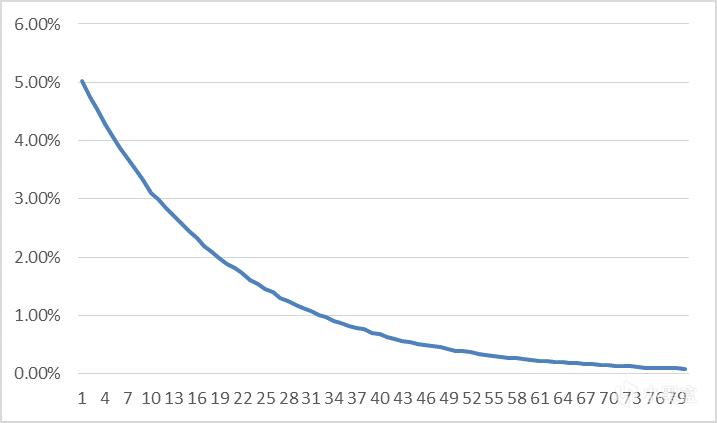
如果这种情况真的发生在玩家群体,无论是快速抽出稀有道具导致玩家消费减少,还是多次不出导致玩家对游戏机制不满,都是游戏运营商不希望看到的。
——————–伪随机:概率分布符合正态分布的算法才是好算法———————-
正态分布只要是学过高中数学的都能有个大概的印象这里不多做赘述(通俗易懂解释正态分布),在市面上游戏中多使用PRD算法和序列填充使得概率与次数的分布图更符合正态分布。
PRD算法:
在游戏War3中,剑圣的暴击发生并不是真的随机概率,而是典型的伪随机算法,具体过程是:假设初始暴击率为A,若第一次未发生暴击,则下一次暴击率为A+A既P(N)=N*A,(N趋于无穷大),以此类推直到暴击发生,则暴击概率回归为A。
PRD最大的好处就在于事件发生次数的标准差比真随机的小(通常真随机算法的事件发生次数的波动范围是PRD的两倍),因此带来了更高的事件发生次数的稳定性,从而更贴近于玩家对概率实际的理解。同时,由于概率的累加,PRD会有一个事件发生时的最大次数,即该次试验时,概率为100%。
PRD优势:解决了两方面的问题,其一,在保持随机的情况下,使事件发生次数更加稳定,
更加符合玩家对概率的认知;其二,拥有一个事件100%发生的次数,无需额外做保底规则。
模拟PRD:假设道具A抽出概率为5%,PRD的暴击基础概率为0.5%,在只考虑单一道具A抽出的情况下,则道具抽出的次数分布图为:
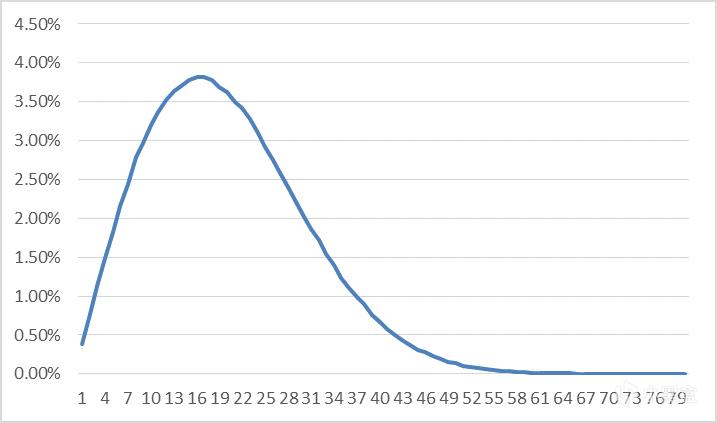
通过图像可以看出,玩家抽出次数的分布接近正态分布,有70%玩家在10-30次抽出道具A,5次以内抽出和40次以上抽出的玩家只有5%,这样可以使得绝大部分玩家体验都在一个可接受的范围内。
但是,对于抽卡来说,一个池子里的道具肯定不止一种,那么在多个道具的情况下如何处理呢?
设定池子中有5个道具,道具A、B、C抽出的概率为5%、10%、15%,道具D、E抽出概率为30%、40%,并且需要道具A、B、C的抽出次数分布均符合正态分布。模拟计算得到道具A、B、C的PRD基础概率分别为0.38%、1.47%、3.2%

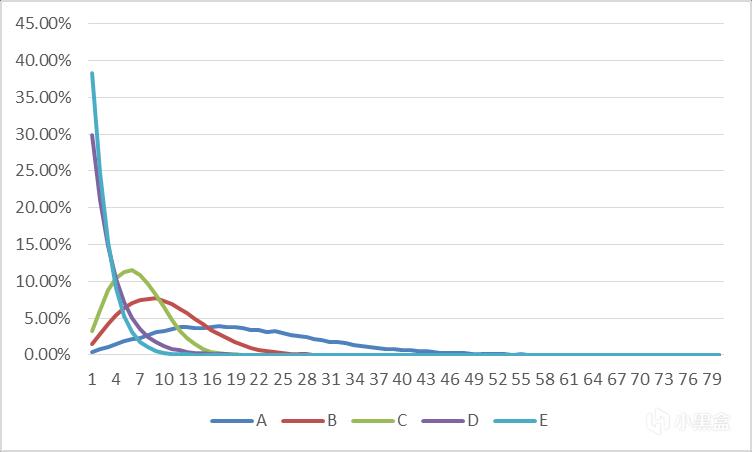
可以看出,五个道具的实际出货概率和设计一致,A、B、C各自的抽出次数分布是大致符合正态分布的,而D、E没有进行PRD算法处理,抽出的曲线和纯随机的曲线一致。
所以,在一个抽卡池中设定一定数量的特殊道具并使特殊道具的抽出次数符合正态分布,。当然也可以通过改进PRD算法(比如乘法换成次方)来调整使得每个道具的抽出次数正态分布曲线更集中。在实际运用中,应该需要配置n个道具的基础概率,配置其余非特殊道具的普通概率,并在每一次玩家抽卡后记录这n个道具距离上次抽出的抽卡次数。(但是,PRD算法总归会让最后一个“保底”道具的抽出次数无法符合正态分布。那么有没有办法可以让池子中所有的道具抽出次数都大致符合正态分布呢?)
用正态分布进行序列填充(DOTA2开箱便是基于此原理但是机制要更复杂)
一个玩家进行多次抽卡,抽出的结果可以看作一个道具的序列,简单列举如下:
[A,B,A,C,D,B,E,D……]
而单个道具的抽出次数,其实可以看作序列中,每一个道具到上一个相同道具的距离。如果这个距离都是符合正态分布的,那么对于这样一个抽出序列,道具的抽出次数应该是符合正态分布的。
那么我们先考虑道具A,设定抽出概率为5%,抽出次数期望为20次,随机生成道具A的抽出次数序列使之符合正态分布如图:
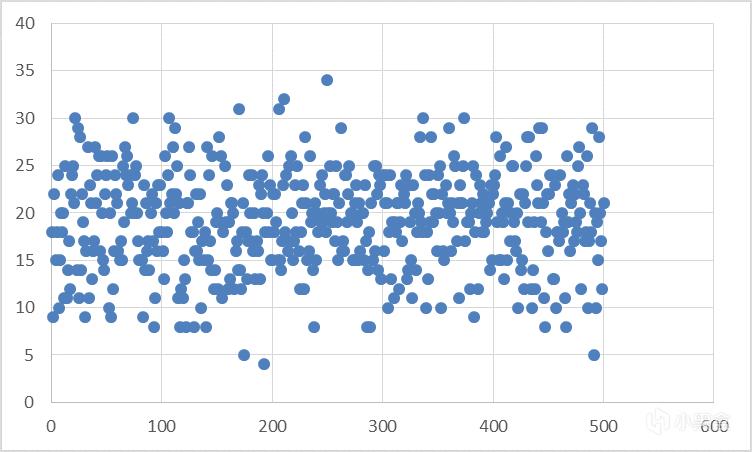
然后,将这些抽出次数,按照顺序插入玩家的抽卡序列中,由于次数符合正态分布,那么在抽卡序列中,抽出次数也会符合正态分布:
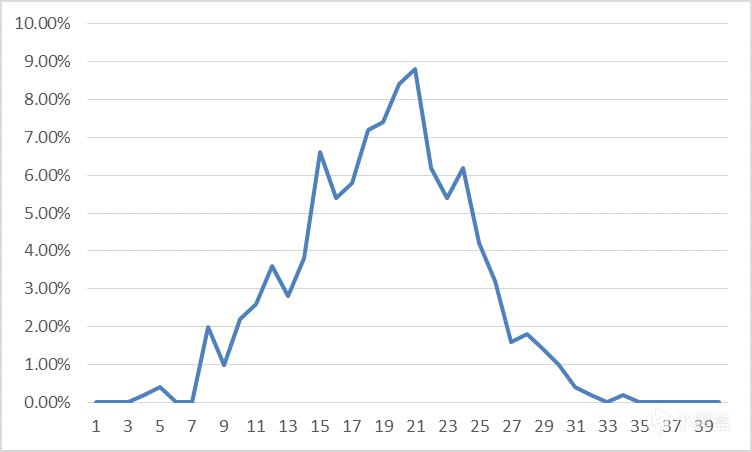
对于单个物品如此计算,而如果池子中有多个物品应该怎么处理呢?还是上面的池子,A、B、C、D、E五个道具分别对应的抽卡概率为5%、10%、15%、30%、40%。那么根据5个道具的抽出次数期望,各生成一个符合正态分布的次数序列,然后按次数大小顺序依次加入抽卡序列中。那么这个抽卡序列应该是所有道具都大致符合正态分布的。
这里需要注意的点是,生成的次数是距离上一次被抽出的次数,所以在每次抽出后,下一个次数应该加上上一个次数,以距离抽卡起点的次数进行比较大小。
情景模拟:
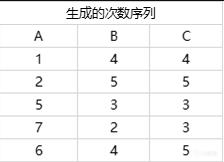
生成3个道具的次数序列,然后按照大小取抽出序列,第一个为A,那么A的第二个值应该加上1变成3,再和B、C进行比较,第二个依然是A,A的第三个值加上3变成8再进行比较,依次进行最后可得到抽卡序列:

请输入图片描述
随机抽卡500万次,5个道具各自的抽出次数分布如图:


我们可以发现5个道具的抽出次数都是大致符合正态分布的,概率和期望也是完全符合设计的。所以用序列填充法是可以完全做到抽卡池中的道具抽出次数都符合正态分布。
当然,序列填充也有一定的问题,在实际运用中,除了配置每个道具各自的概率,也需要记录玩家每一次抽卡后,池子中每一个道具的抽卡次数随机数,并且对于不同的玩家,需要不同的随机种子,不然有可能所有玩家的体验都是一模一样的。
简单总结
一个合理的抽卡数值,既能保持玩家参与抽卡的积极性,又能“杀猪盘式”的氪玩家的钱包。所以数学策划是一个非常重要的方面,能把玩家的欲望玩弄于股掌之间。
而抽卡是卡牌游戏的核心体验,通过改进抽卡概率的算法,优化单个玩家的抽卡体验,使之符合正态分布,PRD算法和序列填充法都是可行的。如果条件允许,从玩家的体验出发优化概率算法,才是这类游戏的长期运营之道
————————————————-分割线—————————————————
如果你觉得这篇文章让你收获了些什么,希望你能点赞加一点盒电。
